Sunlight & Solar Heat

• Solar Stucture
• Fusion Chemistry
• Mass Spectrometry
• Historical Understanding

Fusion Chemistry - A Closer Look

The composition of the sun can be described in several ways. By modern estimates, the composition by mass is: 71% H, 27% He, and 2% other heavier elements. By number of atoms of a given type, the sun's composition is: 91% H, 9% He, and 0.1% other heavier elements. Hydrogen can mean either H atoms or H2 molecules and context is needed to make the meaning of the word clear. In the sun's core neither hydrogen molecules nor neutral hydrogen atoms with one proton in the nucleus and one orbital electron are present. The violent, hot environment of the sun's center rips atoms apart into their constituent pieces: protons, electrons, and other bare atomic nuclei. Hydrogen in the sun's core is ionized, a bare proton, represented by the symbol p+. It is these protons that fuse together with the release of energy.

What keeps the sun from exploding when all of those hydrogen nuclei (protons) collide and fuse together? How has the sun managed to ration its supply of hydrogen nuclei in such a way as to preserve most of them for millions of years? The answer to these questions is that the core, like the rest of the sun, can be regarded as a gaseous body and analyzed according to the principles of the Kinetic Molecular Theory of Gases, which is well understood by researchers.

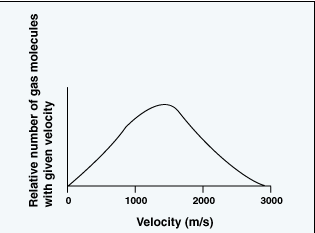
Velocity distribution of particles Courtesy: McREL

In this model the temperature of a moving gas particle is directly proportional to its velocity squared. Also, according to this model there is a bell-shaped statistical distribution of particle velocities in a sample of a gas, as shown here, where the x-axis might represent either particle velocity or particle temperature.

It should be clear that in a sample of gas a few particles are almost motionless, while a few other particles are moving at extraordinarily high velocities. In other words some particles are cold (slow moving) and others are extraordinarily hot (extremely fast moving). However, as indicated by the shape of the curve, the largest portion of particles has a specific velocity that corresponds to the average temperature of the sample. So in the sun's core, even at its average "low" temperature, there are present a relatively few extraordinarily hot protons that are moving with much higher velocities than the "average" proton.

Collision and repulsion of charged particles Courtesy: McREL

Typically, the motion of particles of like charges is random, resulting in collisions and repulsions. It almost seems as if there were a barrier of some kind around each particle, causing repulsion when they approach each other. Only a few super-high-speed protons have enough kinetic energy to tunnel through the electrostatic repulsion barrier and fuse together, initiating the chain of events that ultimately provides the energy from the sun's core. The average proton simply does not have enough energy to tunnel through the barrier and fuse with a collision partner. In other words the vast majority of collisions do not lead to a fusion event.

Proton-proton fusion

In the mid-1930s, after the discovery of the neutron in 1932 and the construction of machines that could accelerate particles, fusion reactions were demonstrated in earth-bound laboratories and the essential correctness of the theoretical predictions regarding fusion in the sun was established. It is now estimated that at core temperatures, only one proton in 100 million is hot enough to fuse during a collision. Put another way, the reaction rate is so very slow that a specific proton would require 14,000 billion years to find a suitably "hot" partner with which to collide in a successful fusion event. Since the sun is only about 4.5 billion years old, most of its protons have not yet found a fusion partner.

How does proton-proton fusion work? First, two exceedingly "hot" protons (hydrogen ions without electrons) collide. This violent event results in the fusion of the two nuclei and the formation of a deuteron, a positron, and a neutrino. This event can be written conveniently in equation form, where superscripts attached to elemental symbols represent mass number and charge:

1H + 1H —> 2D + oe+ + nc

Formation of Deuterium Courtesy: McREL

The symbols oe+ and nc represent a positron and a neutrino, respectively. The deuteron, 2D, differs from a regular hydrogen nucleus in that it contains a neutron in addition to a proton. In this reaction one of the protons has been changed into a neutron, with the formation of a new nucleus containing one proton and one neutron. The key transformation can be written:

1p+ —> 1n0

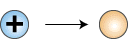
Proton becomes neutron Courtesy: McREL

This equation cannot be correct as written, because it does not account for the charge of the proton. On the left side of the equation is a positive charge and on the right side there is no charge. Note that the mass number is conserved. What is indicated is the creation of a particle having a mass of zero and a charge of plus one on the right side of the equation. Thus we are introduced to the positron, oe+, which is a positively charged electron: a particle of antimatter. More correctly, this equation becomes:

1p+ —> 1no + oe+

Proton becomes neutron and positron Courtesy: McREL

Now charge and mass number are conserved. However, in natural reactions, momentum is also conserved. If a positron speeds away, there must be something that flies out in the opposite direction, since it has been determined that the positron momentum is not balanced by recoil of the proton. A neutrino, answering this requirement, is also emitted. The neutrino is represented by the symbol nc.

The next step in the so-called proton-proton cycle that fuels the sun is the collision of another proton with the deuteron that is formed, producing a helium nucleus containing 2 protons and one neutron, symbolized as 3He.

1H + 2D —> 3He + g

The symbol g represents a gamma ray photon, which is required to balance the energy on both sides of the equation.

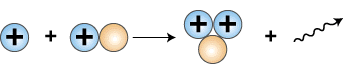
Release of gamma ray photon Courtesy: McREL

Finally, as the last step, two helium-3 nuclei collide to form helium-4, 4He, and two protons.

3He + 3He —> 4He + 2 1H

Formation of helium nucleus Courtesy: McREL

The overall net reaction becomes:

4 1H —> 4He + 2 oe+ + 2 nc + 2 g

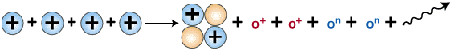
Solar hydrogen fusion yields helium and energy Courtesy: McREL

The only energy production mentioned in the equation above is the gamma rays, which are the original source of the sun's radiated energy. They must eventually work their way out of the core.

The hydrogen nuclei (protons) at the sun's core are hydrogen atoms from which electrons have been ripped away (ionized nuclei). The hot, rapidly moving protons are mixed with an immense number of loose electrons. The positrons formed in the first equation nearly instantaneously encounter their sub-atomic anti-partners, the electrons, instantly annihilating each other and producing a flash of pure energy in the form of gamma ray photons.

oe+ + oe- —> ENERGY

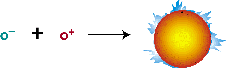
Annihilation of electron and positron Courtesy: McREL

The positron and the electron both have mass (albeit small). Their combined masses are destroyed completely and turned into energy, according to the Einstein relationship E= mc2. Detailed calculations actually show that mass is lost and converted to energy in each of the nuclear reaction steps and these collective mass losses account for the total energy output of the sun.

The scenario outlined above is called the proton-proton chain. It is the most important process for producing the sun's energy, although it is not the only set of reactions that occur.

Other fusion reactions

At even higher temperatures inside the sun and other aging stars, other nuclei undergo fusion reactions. These reactions occur in layers, with the higher temperature layers closer to the center. Some examples are given in the table below.

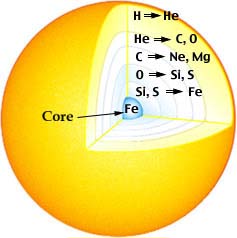
Nuclear Reaction Layers in an Aging Star Courtesy: McREL

Reaction rates

It takes a given proton 14,000 million years to find a "hot" partner. How does the sun's prodigious energy production arise from the proton-proton chain when the reaction rate is so low? The answer is that there are a stupendous number of protons available in the sun. Based on the sun's luminosity and the energy released per proton-proton chain event, the number of core reactions occurring every second is calculated to be about 9 x 1037. The sun's mass is being consumed at the astounding rate of 4.4 x 109 kg per second.

Courtesy: NASA

This mind-boggling number might seem alarming at first glance. Is the sun in danger of running out of hydrogen? No, absolutely not. Presently the mass of the sun is almost 2 x 1030 kg. In other words, the sun still has a lot of hydrogen to work with. In fact, over the 4.5 billion years that the sun has shone, only about 0.03% of its mass has been consumed. The sun is in the middle of its life cycle, and will be heating and lighting the planets for billions of years to come.

Fusion chemistry as described above forms the basis of the Standard Solar Model, an explanation of the sun's composition and functioning used by Genesis scientists in their design of solar wind collection devices. The results of the analysis of the samples of solar wind collected in the Genesis sample return capsule will test the effectiveness of this model in explaining the formation of the solar system.