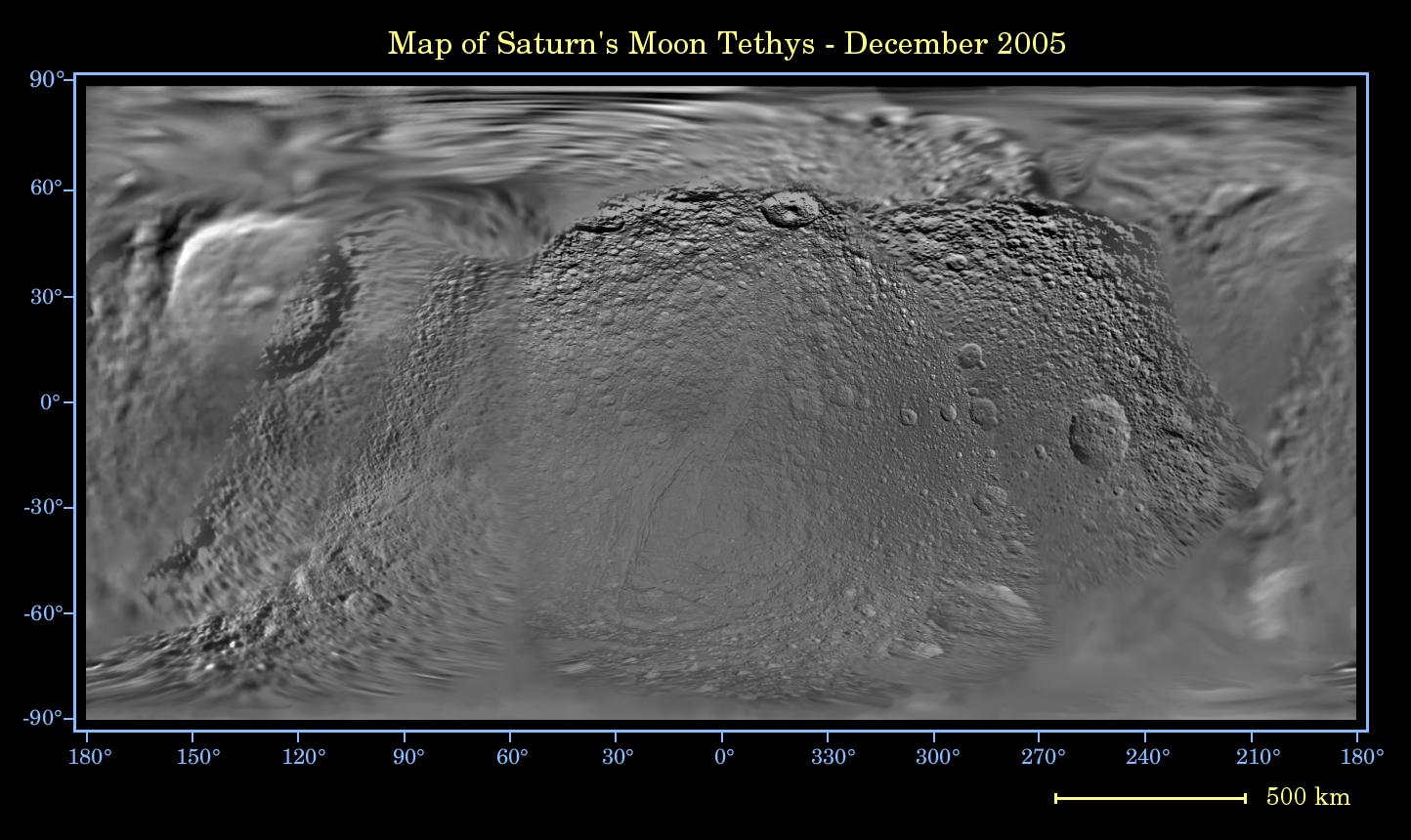
Map of Tethys – December 2005
| PIA Number | PIA07781 |
|---|---|
| Language |
|
This global digital map of Saturn's moon Tethys was created using data taken during Cassini and Voyager spacecraft flybys. The map is an equidistant projection and has a scale of 293 meters (961 feet) per pixel.
The mean radius of Tethys used for projection of this map is 536 kilometers (333 miles). The resolution of the map is 32 pixels per degree.
The Cassini-Huygens mission is a cooperative project of NASA, the European Space Agency and the Italian Space Agency. The Jet Propulsion Laboratory, a division of the California Institute of Technology in Pasadena, manages the mission for NASA's Science Mission Directorate, Washington, D.C. The Cassini orbiter and its two onboard cameras were designed, developed and assembled at JPL. The imaging operations center is based at the Space Science Institute in Boulder, Colo.
For more information about the Cassini-Huygens mission visit http://saturn.jpl.nasa.gov . The Cassini imaging team homepage is at http://ciclops.org .
Credit: NASA/JPL/Space Science Institute
