What are Lagrange Points?
Lagrange Points: What are they?
Lagrange Points are positions in space where the gravitational forces of a two-body system like the Sun and Earth produce enhanced regions of attraction and repulsion. These can be used by spacecraft as "parking spots" in space to remain in a fixed position with minimal fuel consumption.
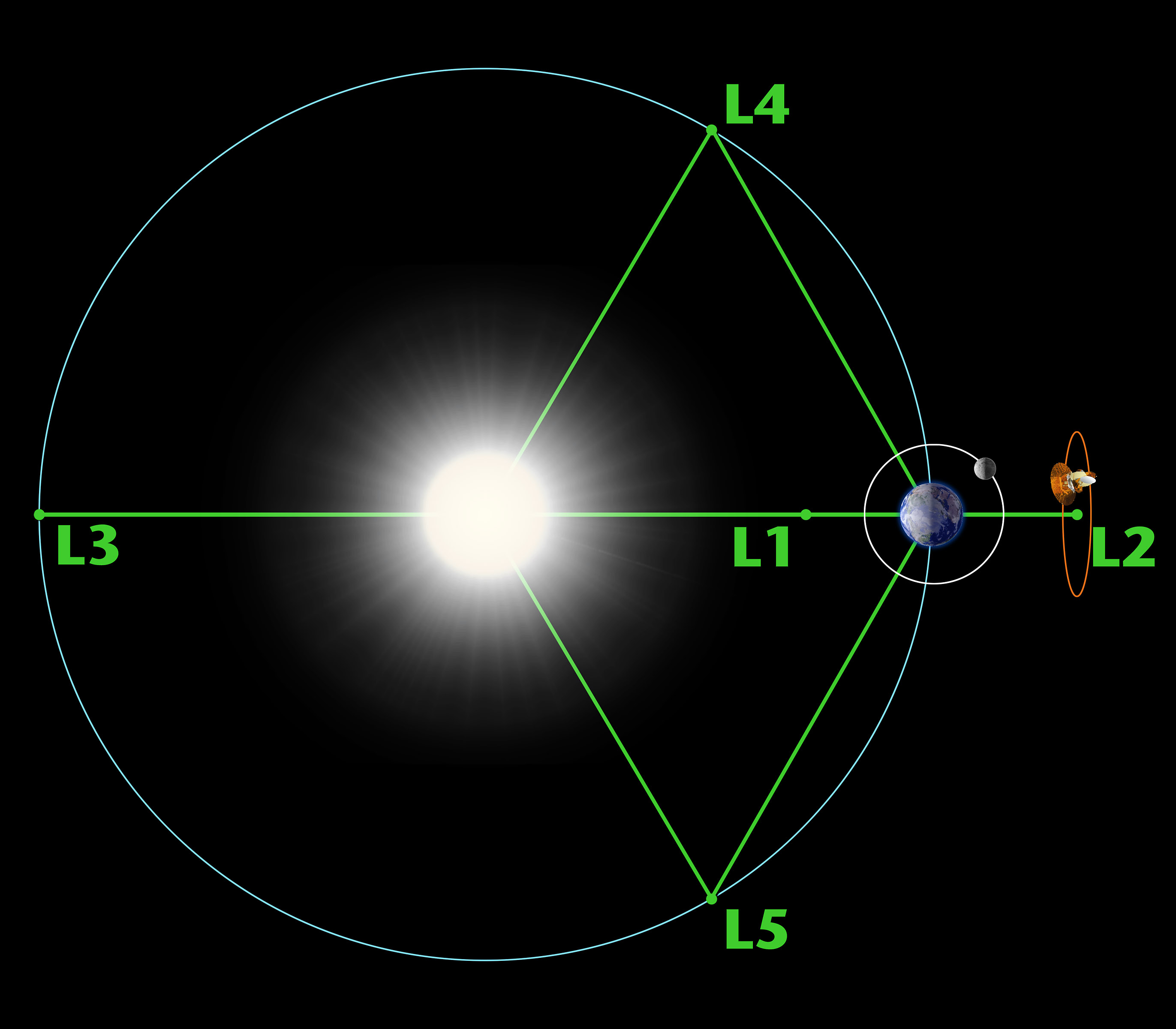
There are five special points where a small mass can orbit in a constant pattern with two larger masses. The Lagrange Points are positions where the gravitational pull of two large masses precisely equals the centripetal force required for a small object to move with them. This mathematical problem, known as the "General Three-Body Problem" was considered by Italian-French mathematician Joseph-Louis Lagrange in his prize-winning paper (Essai sur le Problème des Trois Corps, 1772).
Of the five Lagrange points, three are unstable and two are stable. The unstable Lagrange points – labeled L1, L2, and L3 – lie along the line connecting the two large masses. The stable Lagrange points – labeled L4 and L5 – form the apex of two equilateral triangles that have the large masses at their vertices. L4 leads the orbit of earth and L5 follows.
The L1 point of the Earth-Sun system affords an uninterrupted view of the sun and is currently home to the Solar and Heliospheric Observatory Satellite SOHO. The L2 point of the Earth-Sun system was the home to the WMAP spacecraft, current home of Planck, and future home of the James Webb Space Telescope. L2 is ideal for astronomy because a spacecraft is close enough to readily communicate with Earth, can keep Sun, Earth and Moon behind the spacecraft for solar power and (with appropriate shielding) provides a clear view of deep space for our telescopes. The L1 and L2 points are unstable on a time scale of approximately 23 days, which requires satellites orbiting these positions to undergo regular course and attitude corrections.
NASA is unlikely to find any use for the L3 point since it remains hidden behind the Sun at all times. The idea of a hidden "Planet-X" at the L3 point has been a popular topic in science fiction writing. The instability of Planet X's orbit (on a time scale of 150 years) didn't stop Hollywood from turning out classics like The Man from Planet X.
The L4 and L5 points are home to stable orbits so long as the mass ratio between the two large masses exceeds 24.96. This condition is satisfied for both the Earth-Sun and Earth-Moon systems, and for many other pairs of bodies in the solar system. Objects found orbiting at the L4 and L5 points are often called Trojans after the three large asteroids Agamemnon, Achilles and Hector that orbit in the L4 and L5 points of the Jupiter-Sun system. (According to Homer, Hector was the Trojan champion slain by Achilles during King Agamemnon's siege of Troy).
There are hundreds of Trojan Asteroids in the solar system. Most orbit with Jupiter, but others orbit with Mars. In addition, several of Saturn's moons have Trojan companions. In 1956 the Polish astronomer Kordylewski discovered large concentrations of dust at the Trojan points of the Earth-Moon system. The DIRBE instrument on the COBE satellite confirmed earlier IRAS observations of a dust ring following the Earth's orbit around the Sun. The existence of this ring is closely related to the Trojan points, but the story is complicated by the effects of radiation pressure on the dust grains. In 2010 NASA's WISE telescope finally confirmed the first Trojan asteroid (2010 TK7) around Earth's leading Lagrange point.
Finding the Lagrange Points
The easiest way to understand Lagrange points is to adopt a frame of reference that rotates with the system. The forces exerted on a body at rest in this frame can be derived from an effective potential in much the same way that wind speeds can be inferred from a weather map. The forces are strongest when the contours of the effective potential are closest together and weakest when the contours are far apart.
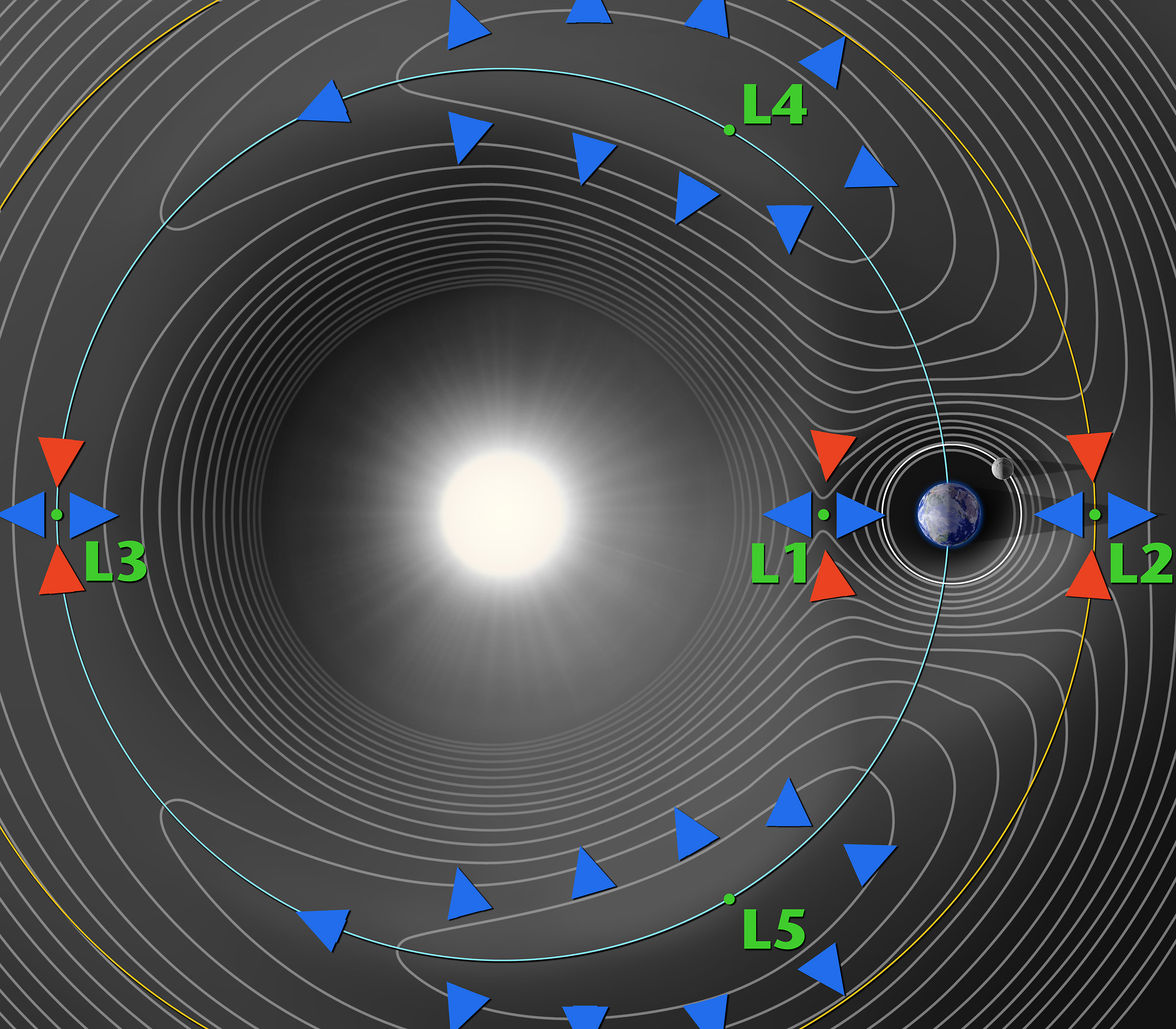
In the above contour plot we see that L4 and L5 correspond to hilltops and L1, L2 and L3 correspond to saddles (i.e. points where the potential is curving up in one direction and down in the other). This suggests that satellites placed at the Lagrange points will have a tendency to wander off (try sitting a marble on top of a watermelon or on top of a real saddle and you get the idea). But when a satellite parked at L4 or L5 starts to roll off the hill it picks up speed. At this point the Coriolis force comes into play - the same force that causes hurricanes to spin up on the earth - and sends the satellite into a stable orbit around the Lagrange point.
Source
- The Lagrange Points
- Download the 1998 original handout with mathematical equations by Neil J. Cornish.